反向传播（英语：Backpropagation，缩写为BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。 在神经网络上执行梯度下降法的主要算法。该算法会先按前向传播方式计算（并缓存）每个节点的输出值，然后再按反向传播遍历图的方式计算损失函数值相对于每个参数的偏导数。

我们将以全连接层，激活函数采用 Sigmoid 函数，误差函数为 Softmax+MSE 损失函数的神经网络为例，推导其梯度传播方式。

准备工作

1、Sigmoid 函数的导数

回顾 sigmoid 函数的表达式：

\[ \sigma(x) =\frac{1}{1+e^{-x}} \]

其导数为：

\[ \frac{d}{dx}\sigma(x) =\frac{d}{dx} \left(\frac{1}{1+e^{-x}} \right) \]

\[ =\frac{e^{-x}}{(1+e^{-x})^2} \]

\[ =\frac{(1 + e^{-x})-1}{(1+e^{-x})^2} \]

\[ =\frac{1+e^{-x}}{(1+e^{-x})^2} - \left(\frac{1}{1+e^{-x}}\right)^2 \]

\[ =\sigma(x) - \sigma(x)^2 \]

\[ =\sigma(1-\sigma) \]

可以看到,Sigmoid 函数的导数表达式最终可以表达为激活函数的输出值的简单运算,利
用这一性质,在神经网络的梯度计算中,通过缓存每层的 Sigmoid 函数输出值,即可在需
要的时候计算出其导数。Sigmoid 函数导数的实现：

import numpy as np # 导入 numpy

def sigmoid(x): # sigmoid 函数
	return 1 / (1 + np.exp(-x))

def derivative(x): # sigmoid 导数的计算
	return sigmoid(x)*(1-sigmoid(x))

2、均方差函数梯度

均方差损失函数表达式为： $\( L =\frac{1}{2}\sum_{k=1}^{K}(y_k-o_k)^2 \)\( 其中 \) y_k \( 为真实值， \) o_k \( 为输出值。则它的偏导数 \) \frac{\partial L}{\partial o_i} $ 可以展开为：

\[ \frac{\partial L}{\partial o_i} =\frac{1}{2}\sum_{k=1}^{K}\frac{\partial}{\partial o_i}(y_k - o_k)^2 \]

利用链式法则分解为

\[ \frac{\partial L}{\partial o_i} =\frac{1}{2}\sum_{k=1}^{K}\cdot2\cdot(y_k-o_k)\cdot\frac{\partial(y_k-o_k)}{\partial o_i} \]

\[ \frac{\partial L}{\partial o_i} =\sum_{k=1}^{K}(y_k-o_k)\cdot(-1)\cdot\frac{\partial o_k}{\partial o_i} \]

\[ \frac{\partial o_k}{\partial o_i}\]

仅当 k =i 时才为 1,其他点都为 0, 也就是说 \( \frac{\partial o_k}{\partial o_i} \) 只与第 i 号节点相关，与其他节点无关，因此上式中的求和符号可以去掉，均方差的导数可以推导为

\[ \frac{\partial L}{\partial o_i} =(o_i - y_i) \]

3、单个神经元梯度

对于采用 Sigmoid 激活函数的神经元模型,它的数学模型可以写为

\[ o^1 =\sigma(w^1x+b^1) \]

其中

• 变量的上标表示层数，如 \( o^1 \) 表示第一个隐藏层的输出

• x 表示网络的输入

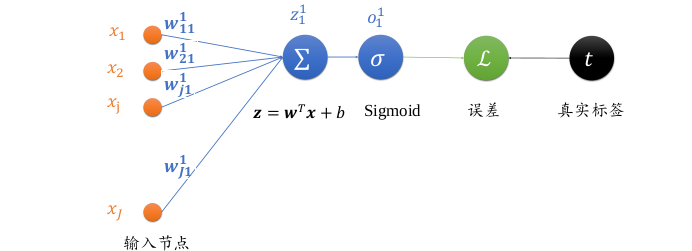
单个神经元模型如下图所示

• 输入节点数为 J

  • 其中输入第 \( j \) 个节点到输出 \( o^1 \) 的权值连接记为 \( w^1_{j1} \)

• 上标表示权值属于的层数，下标表示当前连接的起始节点号和终止节点号

  • 如下标 \( j1 \) 表示上一层的第 \( j \) 号节点到当前层的 1 号节点

• 未经过激活函数的输出变量为 \( z_1^1 \) ，经过激活函数之后的输出为 \( o_1^1 \)

• 由于只有一个输出节点，故 \( o_1^1 =o^1 \)

下面我们来计算均方差算是函数的梯度

由于单个神经元只有一个输出，那么损失函数可以表示为

\[ L =\frac{1}{2}(o_1^1 - t)^2 \]

添加 \( \frac{1}{2} \) 是为了计算方便，我们以权值连接的第 \( j\in[1,J] \) 号节点的权值 \( w_{j1} \) 为例，考虑损失函数 \( L \) 关于 \( w_{j1} \) 的偏导数，即 对其的偏导数 \( \frac{\partial L}{\partial w_{j1}} \)

\[ \frac{\partial L}{\partial w_{j1}} =(o_1 - t)\frac{\partial o_1}{\partial w_{j1}} \]

由于 \( o_1 =\sigma(z_1) \) ，由上面的推导可知 Sigmoid 函数的导数 \( \sigma' =\sigma(1-\sigma) \)

\[ \frac{\partial L}{\partial w_{j1}} =(o_1 - t)\frac{\partial \sigma(z_1)}{\partial w_{j1}} \]

\[ =(o_1-t)\sigma(z_1)(1-\sigma(z_1))\frac{\partial z_1}{\partial w_{j1}} \]

把 \( \sigma(z_1) \) 写成 \( o_1 \)

\[ =(o_1-t)o_1(1-o_1)\frac{\partial z_1}{\partial w_{j1}} \]

由于 \( \frac{\partial z_1}{\partial w_{j1}} =x_j \)

\[ \frac{\partial L}{\partial w_{j1}} =(o_1-t)o_1(1-o_1)x_j \]

从上式可以看到,误差对权值 \( w_{j1} \) 的偏导数只与输出值 \( o_1 \) 、真实值 t 以及当前权值连接的输入 \( x_j \) 有关

4、全链接层梯度

我们把单个神经元模型推广到单层全连接层的网络上,如下图所示。输入层通过一个全连接层得到输出向量 \( o^1 \) ,与真实标签向量 t 计算均方差。输入节点数为 \( J \) ,输出节点数为 K 。

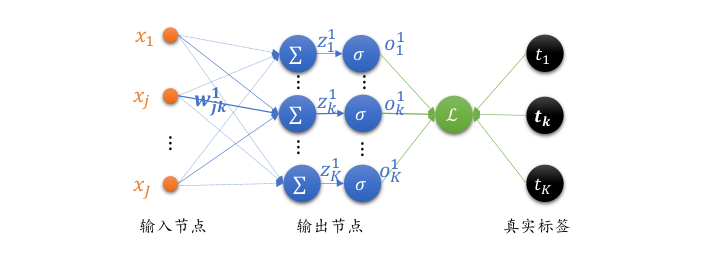
与单个神经元不同，全链接层有多个输出节点 \( o_1^1, o_2^1, o_3^1,...,o_K^1 \) ，每个输出节点对应不同真实标签 \( t_1, t_2, t_3,..., t_K \) ，均方误差可以表示为

\[ L =\frac{1}{2}\sum_{i=1}^K(o_i^1-t_i)^2 \]

由于 \( \frac{\partial L}{\partial w_{jk}} \) 只与 \( o_k^1 \) 有关联，上式中的求和符号可以去掉，即 \( i =k \)

\[ \frac{\partial L}{\partial w_{jk}} =(o_k-t_k)\frac{\partial o_k}{\partial w_{jk}} \]

将 \( o_k=\sigma(z_k) \) 带入

\[ \frac{\partial L}{\partial w_{jk}} =(o_k-t_k)\frac{\partial \sigma(z_k)}{\partial w_{jk}} \]

考虑 \( Sigmoid \) 函数的导数 \( \sigma' =\sigma(1-\sigma) \)

\[ \frac{\partial L}{\partial w_{jk}} =(o_k-t_k)\sigma(z_k)(1-\sigma(z_k))\frac{\partial z_k^1}{\partial w_{jk}} \]

将 \( \sigma(z_k) \) 记为

\( o_k \)

\[ \frac{\partial L}{\partial w_{jk}} =(o_k-t_k)o_k(1-o_k)\frac{\partial z_k^1}{\partial w_{jk}} \]

最终可得 $\( \frac{\partial L}{\partial w_{jk}} =(o_k-t_k)o_k(1-o_k)\cdot x_j \)\( 由此可以看到,某条连接 \) w_{jk} \( 上面的连接,只与当前连接的输出节点 \) o_k^1 \( ,对应的真实值节点的标签 \) t_k^1 $ ,以及对应的输入节点 x 有关。

我们令 \( \delta_k =(o_k-t_k)o_k(1-o_k) \) ，则 \( \frac{\partial L}{\partial w_{jk}} \) 可以表达为 $\( \frac{\partial L}{\partial w_{jk}}=\delta_k\cdot x_j \)\( 其中 \) \delta k \( 变量表征连接线的终止节点的梯度传播的某种特性，使用 \) \delta_k \( 表示后， \) \frac{\partial L}{\partial w{jk}} \( 偏导数只与当前连接的起始节点 \) x_j \( ，终止节点处 \) \delta_k $ 有关，理解起来比较直观。

5、反向传播算法

看到这里大家也不容易，毕竟这么多公式哈哈哈，不过激动的时刻到了

先回顾下输出层的偏导数公式

\[ \frac{\partial L}{\partial w_{jk}} =(o_k-t_k)o_k(1-o_k)\cdot x_j =\delta_k \cdot x_j \]

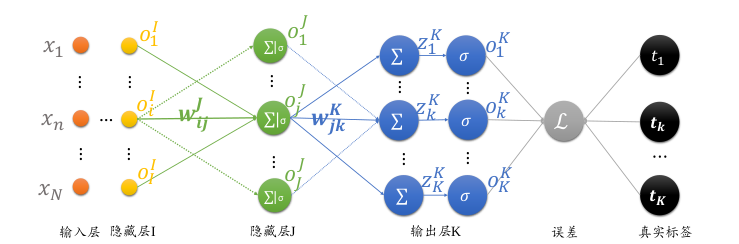
多层全连接层如下图所示

• 输出节点数为 K ，输出 \( o^k =[o_1^k, o_2^k, o_3^k,..., o_k^k] \)

• 倒数的二层的节点数为 J ，输出为 \( o^J=[o_1^J, o_2^J,..., o_J^J] \)

• 倒数第三层的节点数为 I ，输出为 \( o^I =[o_1^I, o_2^I,..., o_I^I] \)

均方误差函数

\[ \frac{\partial L}{\partial w_{ij}}=\frac{\partial}{\partial w_{ij}}\frac{1}{2}\sum_{k}(o_k-t_k)2 \]

由于 \( L \) 通过每个输出节点 \( o_k \) 与 \( w_i \) 相关联,故此处不能去掉求和符号

\[ \frac{\partial L}{\partial w_{ij}}=\sum_k(o_k-t_k)\frac{\partial o_k}{\partial w_{ij}} \]

将 \( o_k=\sigma(z_k) \) 带入

\[ \frac{\partial L}{\partial w_{ij}}=\sum_k(o_k-t_k)\frac{\partial \sigma(z_k)}{\partial w_{ij}} \]

\( Sigmoid \) 函数的导数 \( \sigma' =\sigma(1-\sigma) \) ，继续求导，并将 \( \sigma(z_k) \) 写回 \( o_k \)

\[ \frac{\partial L}{\partial w_{ij}}=\sum_k(o_k-t_k)o_k(1-o_k)\frac{\partial z_k}{\partial w_{ij}} \]

对于 \( \frac{\partial z_k}{\partial w_{ij}} \) 可以应用链式法则分解为

\[ \frac{\partial z_k}{\partial w_{ij}} =\frac{\partial z_k}{o_j}\cdot \frac{\partial o_j}{\partial w_{ij}} \]

由图可知 \( \left(z_k =o_j \cdot w_{jk} + b_k\right) \) ,故有

\[ \frac{\partial z_k}{o_j} =w_{jk} \]

所以

\[ \frac{\partial L}{\partial w_{ij}}=\sum_k(o_k-t_k)o_k(1-o_k)w_{jk}\cdot\frac{\partial o_j}{\partial w_{ij}} \]

考虑到 \( \frac{\partial o_j}{\partial w_{ij}} \) 与 k 无关，可将其提取出来

\[ \frac{\partial L}{\partial w_{ij}}=\frac{\partial o_j}{\partial w_{ij}}\cdot\sum_k(o_k-t_k)o_k(1-o_k)w_{jk} \]

再一次有 \( o_k=\sigma(z_k) \) ，并利用 \( Sigmoid \) 函数的导数 \( \sigma' =\sigma(1-\sigma) \) 有

\[ \frac{\partial L}{\partial w_{ij}}=o_j(1-o_j)\frac{\partial z_j}{\partial w_{ij}} \cdot\sum_k(o_k-t_k)o_k(1-o_k)w_{jk} \]

由于 \( \frac{\partial z_j}{\partial w_{ij}} =o_i \left(z_j =o_i\cdot w_{ij} + b_j\right) \)

\[ \frac{\partial L}{\partial w_{ij}}=o_j(1-o_j)o_i \cdot\sum_k(o_k-t_k)o_k(1-o_k)w_{jk} \]

其中 \( \delta _k^K =(o_k-t_k)o_k(1-o_k) \) ，则

\[ \frac{\partial L}{\partial w_{ij}}=o_j(1-o_j)o_i \cdot\sum_k\delta _k^K\cdot w_{jk} \]

仿照输出层的书写方式，定义

\[ \delta_j^J =o_j(1-o_j) \cdot \sum_k \delta _k^K\cdot w_{jk} \]

此时 \( \frac{\partial L}{\partial w_{ij}} \) 可以写为当前连接的起始节点的输出值 \( o_i \) 与终止节点 \( j \) 的梯度信息 \( \delta _j^J \) 的简单相乘运算:

\[ \frac{\partial L}{\partial w_{ij}} =\delta_j^J\cdot o_i^I \]

通过定义 \( \delta \) 变量,每一层的梯度表达式变得更加清晰简洁,其中 \( \delta \) 可以简单理解为当前连接 \( w_{ij} \) 对误差函数的贡献值。

6、总结

输出层

\[ \frac{\partial L}{\partial w_{jk}} =\delta _k^K\cdot o_j \]

\[ \delta _k^K =(o_k-t_k)o_k(1-o_k) \]

倒数第二层：

\[ \frac{\partial L}{\partial w_{ij}} =\delta _j^J\cdot o_i \]

\[ \delta_j^J =o_j(1-o_j) \cdot \sum_k \delta _k^K\cdot w_{jk} \]

倒数第三层：

\[ \frac{\partial L}{\partial w_{ni}} =\delta _i^I\cdot o_n \]

\[ \delta _i^I =o_i(1-o_i)\cdot \sum_j\delta_j^J\cdot w_{ij} \]

其中 \( o_n \) 为倒数第三层的输入，即倒数第四层的输出

依照此规律,只需要循环迭代计算每一层每个节点的 \( \delta _k^K, \delta_j^J, \delta_i^I,... \) 等值即可求得当前层的偏导数,从而得到每层权值矩阵 \( W \) 的梯度,再通过梯度下降算法迭代优化网络参数即可。