二次型与矩阵#
二次型与矩阵对应关系#
\[\begin{split}
\begin{aligned}
f(x)&=a_{11}x_1^2 + a_{22}x_2^2 + \cdots + a_{nn}x_n^2 \\
&+ 2a_{12}x_1x_2 + 2a_{13}x_1x_3 + \cdots + 2a_{n-1,n}x_{n-1}x_n
\end{aligned}
\end{split}\]
观察各个项，行和列按 \(x_1,x_2,x_3,\cdots,x_n\) 的顺序排列成表格，每个格子内为行列相乘的项，平方项恰在对角线位置，其他项放在对角线上三角区域，可以得到下面方阵：
\[\begin{split}
\begin{aligned}
\begin{array}{c:ccccc}
& x_1 & x_2 & x_3 & \cdots & x_n \\
\hdashline
x_1 & a_{11}x_1^2 & 2a_{12}x_1x_2 & 2a_{13}x_1x_3& \cdots & 2a_{1n}x_1x_n \\
x_2& 0 & a_{22}x_2^2 & 2a_{23}x_2x_3& \cdots & 2a_{2n}x_2x_n \\
x_3& 0 & 0 & a_{33}x_3^2& \cdots & 2a_{3n}x_3x_n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\
x_n& 0 & 0 & 0 & \cdots & a_{nn}x_n^2 \end{array}
\end{aligned}
\end{split}\]
如果把像 \(2a_{12} , 2a_{13},\dots,2a_{(n-1)n}\) 这样的2倍的系数沿着对角线对称的位置拆分放置，即 \(a_{12}=a_{21} , a_{13}=a_{31},\dots,a_{(n-1)n}=a_{n(n-1)}\) ，那么可以得到下面的样子：
\[\begin{split}
\begin{aligned}
\begin{array}{c:ccccc}
& x_1 & x_2 & x_3 & \cdots & x_n \\
\hdashline
x_1 & a_{11}x_1^2 & a_{12}x_1x_2 & a_{13}x_1x_3& \cdots & a_{1n}x_1x_n \\
x_2& a_{21}x_1x_2 & a_{22}x_2^2 & a_{23}x_2x_3& \cdots & a_{2n}x_2x_n \\
x_3& a_{31}x_1x_3 & a_{32}x_2x_3 & a_{33}x_3^2& \cdots & a_{3n}x_3x_n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\
x_n& a_{n1}x_1x_n & a_{n2}x_2x_n & a_{n3}x_3x_n & \cdots & a_{nn}x_n^2 \end{array}
\end{aligned}
\end{split}\]
即
\[\begin{split}
\begin{aligned}
f(x) &=x_1(a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n \\
& +x_2(a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n) \\
& +x_3(a_{31}x_1 + a_{32}x_2 + \cdots + a_{3n}x_n) \\
& + \cdots\\
& + x_n(a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n) \\
\end{aligned}
\end{split}\]
写成矩阵相乘的方式为：
\[\begin{split}
\begin{aligned}
f(x)&= (x_1, x_2, \cdots, x_n) \begin{pmatrix}a_{11}x_1 & a_{12}x_2 & \cdots & a_{1n}x_n \\ a_{21}x_1 & a_{22}x_2 & \cdots & a_{2n}x_n \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1}x_1 & a_{n2}x_2 & \cdots & a_{nn}x_n \end{pmatrix}\\
&=(x_1, x_2, \cdots, x_n)\begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}\begin{pmatrix}x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} \\
&=x^TAx
\end{aligned}
\end{split}\]
其中
\[\begin{split}
A=\begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix} , x=\begin{pmatrix}x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}
\end{split}\]
二次型 \(f(x)\) ，和矩阵表示 \(x^TAx\) 是等价的。二次型可以通过配方法换元标准化。然而，只有表示成对称矩阵才可以的对角化为标准形。
那么怎么理解二次型如果表示为非对称矩阵为什么不能对角化呢？明明是等价的表示。例如， \(x_1^2 + x_2^2 + 2x_1x_2\) 如果表示为
\[\begin{split}
\begin{aligned}
A=\begin{pmatrix}
1 & 1 \\
1 & 1
\end{pmatrix} \\
B=\begin{pmatrix}
1 & 2 \\
0 & 1
\end{pmatrix}\\
C=\begin{pmatrix}
1 & 0 \\
2 & 1
\end{pmatrix}
\end{aligned}
\end{split}\]
B和C只是交换了位置，只讨论A、B两个矩阵的对角化。其特征值分别为0或2、重根1。
A的特征值为2、0，特征向量分别为：
\[\begin{split}
\begin{pmatrix}1 \\ 1\end{pmatrix},
\begin{pmatrix}-1 \\ 1\end{pmatrix}
\end{split}\]
所以，
\[\begin{split}
\begin{aligned}
P&=\begin{pmatrix}1 & -1 \\ 1 & 1\end{pmatrix} \\
P^{-1}&=\begin{pmatrix}\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2}\end{pmatrix}\\
\end{aligned}
\end{split}\]
那么，
\[\begin{split}
\begin{aligned}
P^{-1}AP&=\begin{pmatrix}\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2}\end{pmatrix}\begin{pmatrix}1 & 1 \\ 1 & 1\end{pmatrix}\begin{pmatrix}1 & -1 \\ 1 & 1\end{pmatrix}\\
&=\begin{pmatrix}2 & 0 \\ 0 & 0\end{pmatrix}
\end{aligned}
\end{split}\]
若 \(x=Py\) ， \(x^T=(Py)^T=y^TP^T\) 。
但由于此时的 \(P\) 未经酉变换， \(P^{-1}\neq P^T\) ，所以 \(y^T(P^{-1}AP)y\neq diag(2,0)\)
将 \(P\) 矩阵转换为酉变换，
\[\begin{split}
\begin{aligned}
U&=\begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{pmatrix} \\
U^{-1}&=\begin{pmatrix}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{pmatrix}\\
&=U^T
\end{aligned}
\end{split}\]
即
\[
\begin{aligned}
f(y_1,y_2)&=2y_1^2+0y_2^2
\end{aligned}
\]
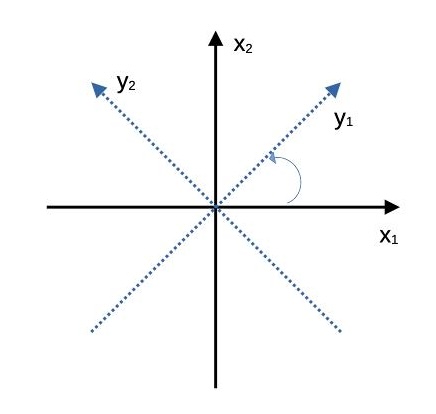
此时对应的换元关系为：
\[\begin{split}
\begin{aligned}
\begin{pmatrix}x_1 \\ x_2\end{pmatrix}=U\begin{pmatrix}y_1 \\ y_2\end{pmatrix}=\begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{pmatrix}\begin{pmatrix}y_1 \\ y_2\end{pmatrix}\\
\Rightarrow
\left\{
\begin{aligned}
x_1=\frac{1}{\sqrt{2}}y_1-\frac{1}{\sqrt{2}}y_2 \\
x_2=\frac{1}{\sqrt{2}}y_1+\frac{1}{\sqrt{2}}y_2
\end{aligned}
\right.
\end{aligned}
\end{split}\]
\[\begin{split}
\begin{aligned}
\begin{pmatrix}y_1 \\ y_2\end{pmatrix}=U^{-1}\begin{pmatrix}x_1 \\ x_2\end{pmatrix}=U^{T}\begin{pmatrix}x_1 \\ x_2\end{pmatrix}=\begin{pmatrix}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{pmatrix}\begin{pmatrix}x_1 \\ x_2\end{pmatrix}\\
\Rightarrow
\left\{
\begin{aligned}
y_1&=\frac{1}{\sqrt{2}}x_1+\frac{1}{\sqrt{2}}x_2 \\
y_2&=-\frac{1}{\sqrt{2}}x_1+\frac{1}{\sqrt{2}}x_2
\end{aligned}
\right.
\end{aligned}
\end{split}\]
如何理解这种变换呢？#
这种变换，将坐标轴旋转45度，如下图。
与配方法对照#
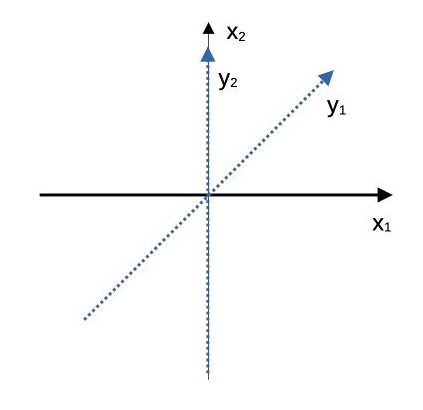
对于上面的简单的二次型，很显然可以做 \(y_1=x_1+x_2\) 的换元，和 \(y_2\) 没有关系，可以取任意值，如果取 \(y_2=x_2\) 。得到的结果为：
\[
f(x_1,x_2)=x_1^2+x_2^2+2x_1x_2=(x_1+x_2)^2=y_1^2
\]
取
\[\begin{split}
\begin{aligned}
A=\begin{pmatrix}
1 & 1 \\
1 & 1
\end{pmatrix}
\end{aligned}
\end{split}\]
此时的变换关系为：
\[\begin{split}
\begin{pmatrix}y_1 \\ y_2\end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 0 & 1\end{pmatrix}\begin{pmatrix}x_1 \\ x_2\end{pmatrix}=Q\begin{pmatrix}x_1 \\ x_2\end{pmatrix}
\end{split}\]
那么，
\[\begin{split}
\begin{aligned}
\begin{pmatrix}x_1 \\ x_2\end{pmatrix}
&=Q^{-1}\begin{pmatrix}y_1 \\ y_2\end{pmatrix} \\
&=\begin{pmatrix} 1 & -1 \\ 0 & 1\end{pmatrix}\begin{pmatrix}y_1 \\ y_2\end{pmatrix}\\
D&=\begin{pmatrix} 1 & -1 \\ 0 & 1\end{pmatrix}
\end{aligned}
\end{split}\]
即
\[\begin{split}
\left\{
\begin{aligned}
x_1&=y_1-y_2 \\
x_2&=y_2
\end{aligned}
\right.
\end{split}\]
\[\begin{split}
\begin{aligned}
f(x)&=x^TAx=(Dy)^TADy=y^TD^TADy\\
&=y^T\begin{pmatrix} 1 & 0 \\ -1 & 1\end{pmatrix}\begin{pmatrix}
1 & 1 \\
1 & 1
\end{pmatrix}\begin{pmatrix} 1 & -1 \\ 0 & 1\end{pmatrix}y \\
&=y_1^2
\end{aligned}
\end{split}\]
显然此处 \( D^T \neq D^{-1} \) ，虽然可以变换成了标准形，但是并不是 \(diag(2,0)\) 的形式， \(D\) 也不是特征向量矩阵。并且 \(D\) 不是正规矩阵，不能做酉变换。 \( D^T \neq D^{-1} \) ，此变换不能和特征向量和特征值建立联系。
如何理解这种变换呢？#
这种变换效果如下图，变换后的坐标轴成45度角，并且和 \(y_2\) 无关。
如果矩阵为B#
其特征值为重根1，仅对应一个特征向量，无法对角化。但是二次型还是那个式子，为什么却不能对角化呢？ 二次型和对称矩阵具有相同的计算特性，计算出来的特征向量恰好和换元变换关系。 \(D^T\) 表示换元变换关系， \(D^{-1}\) 表示特征值和特征向量关系， \(D^T=D^{-1}\) 将特征值特征向量关系和换元关系联系了起来。