月食和日食计算#

基本参数#

地球公转周期 365.2564 天
月球公转周期 27.32166 天
月球轨道面与地球轨道面交角 \(\alpha=5°09'\)
地球和月球都是椭圆轨道，但是考虑离心率都很小，可以近似为圆形。

计算思路#

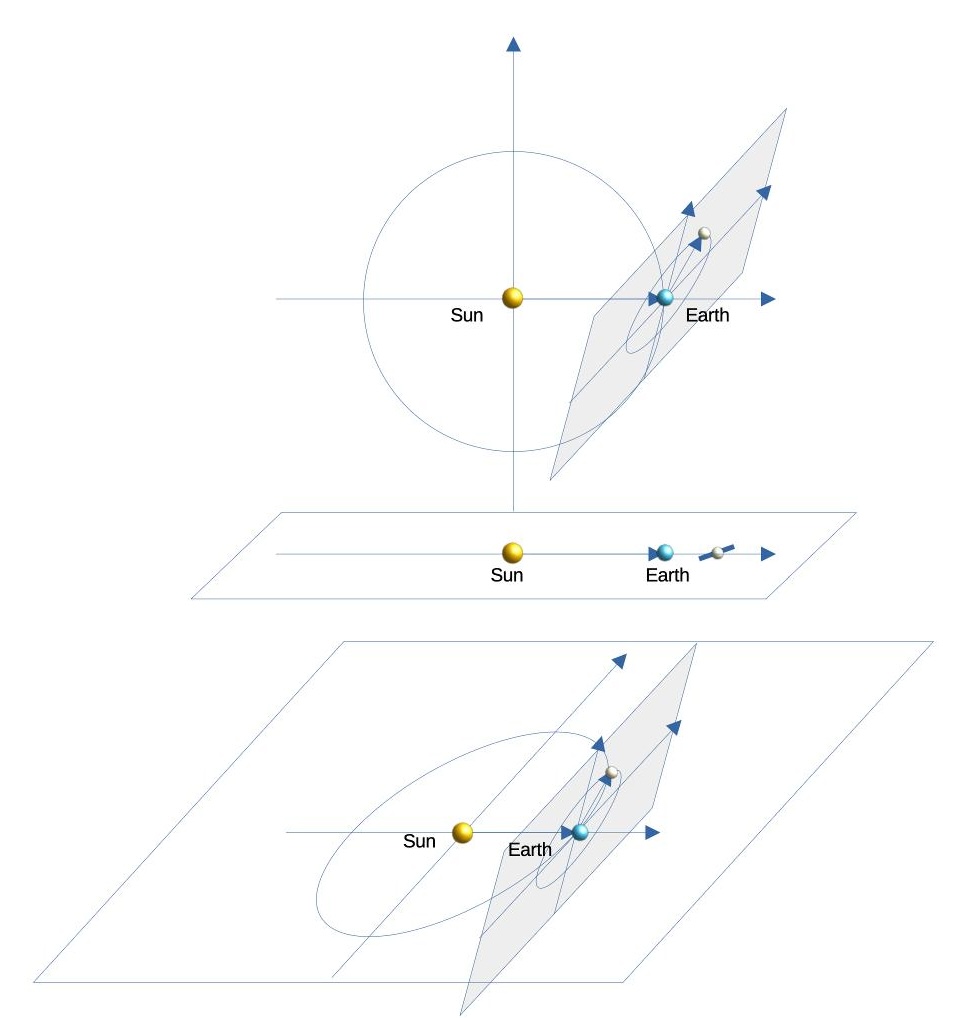
计算月食或者日食即计算向量 \(\overrightarrow{SunEarth}\) 和 \(\overrightarrow{EarthMoon}\) 的夹角如果接近0，即太阳、地球、月球一线月食发生。类似，若夹角180度，即日食发生。

计算#

\[\begin{split} \begin{aligned} \overrightarrow{SunEarth} = R * [cos(\omega_{1} t+ \frac {\pi}{2}) , sin(\omega_{1} t+ \frac {\pi}{2}), 0] \\ \overrightarrow{EarthMoon} = r * [cos(\omega_{2} t+ \frac {\pi}{2}) cos\alpha , sin(\omega_{2} t+ \frac {\pi}{2}), sin(\omega_{2} t+ \frac {\pi}{2}) sin\alpha] \end{aligned} \end{split}\]

其中， \(\omega_{1}\) 是地球公转角速度， \(\omega_{1}\) 是月球公转角速度。 \(R\) 是地球公转半径， \(r\) 月球公转半径。向量之间的夹角为 \(\beta\)

\[\begin{split} \begin{aligned} cos\beta &=\frac{\overrightarrow{SunEarth} \cdot \overrightarrow{SunEarth}} {|\overrightarrow{SunEarth}|*|\overrightarrow{SunEarth}|} \\ &=\frac{\overrightarrow{SunEarth} \cdot \overrightarrow{SunEarth}} {Rr} \\ &=\frac{Rr[sin(\omega_{1}t)sin(\omega_{2}t)cos\alpha + cos(\omega_{1}t)cos(\omega_{2}t)]}{Rr} \\ &=sin(\omega_{1}t)sin(\omega_{2}t)cos\alpha + cos(\omega_{1}t)cos(\omega_{2}t) \end{aligned} \end{split}\]

当 \(1-cos\beta <= \delta\) 时，可认为近似夹角为0。

解方程#

从网上查到月食、日食数据，以20250908为参考点

日期	描述	距离20250908天数
20250314	月食	-178
20250908	月全食	0
20250922	日偏食*	14
20260217	日环食*	162
20260303	月食	176
20260813	日全食*	339
20260828	月偏食	354
20270206	日环食*	516
20270221	半影月食	531
20270719	半影月食	679
20270802	日全食*	693
20270817	半影月食	708
20281231	月食	1210
20290626	月食	1387
20291221	月食	1565